Koliko osi simetrije ima krug?
osi simetrije kruga Oni su beskonačni. Ove osi su one koje dijele bilo koji geometrijski oblik na dva točno jednaka pola.
A krug se sastoji od svih točaka čija je udaljenost do fiksne točke manja ili jednaka određenoj vrijednosti "r".
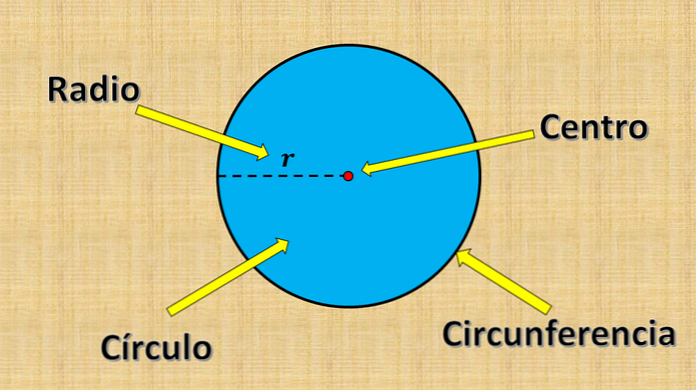
Gore navedena fiksna točka naziva se središte, a vrijednost "r" se naziva radijus. Polumjer je najveća udaljenost između točke na krugu i središta.
S druge strane, bilo koji segment čije su krajevi na rubu kruga (opseg) i prolazeći kroz središte nazivaju se promjerom. Njegovo mjerenje je uvijek jednako dvostrukom radijusu.
Krug i opseg
Nemojte brkati krug s krugom. Obuhvat se odnosi samo na točke koje su na udaljenosti "r" od središta; to jest, samo rub kruga.
Međutim, kada tražite osi simetrije, ravnodušni ste ako radite s krugom ili krugom.
Što je os simetrije?
Os simetrije je pravac koji na dva jednaka dijela dijeli određenu geometrijsku figuru. Drugim riječima, os simetrije djeluje poput zrcala.
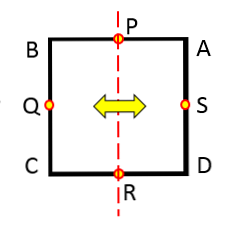
Osovine simetrije kruga
Ako promatrate bilo koji krug, bez obzira na njegov radijus, možete vidjeti da ne svaka linija koja prelazi to je os simetrije.
Primjerice, nijedna linija koja je nacrtana na sljedećoj slici nije os simetrije.
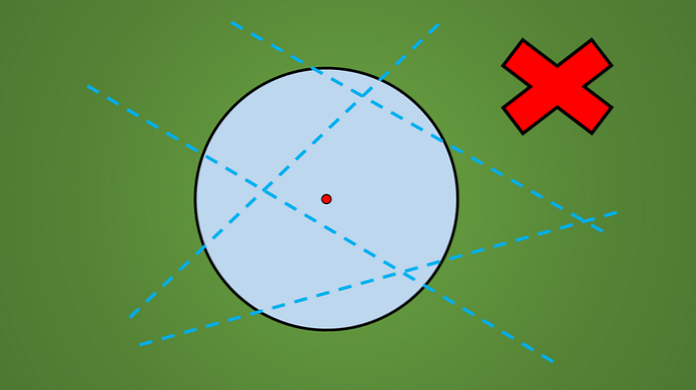
Jednostavan način za provjeru je li crta os simetrije ili ne, mora odražavati okomitu geometrijsku figuru na suprotnu stranu linije.
Ako se refleksija ne uklapa s izvornom figurom, tada ta linija nije os simetrije. Sljedeća slika prikazuje ovu tehniku.
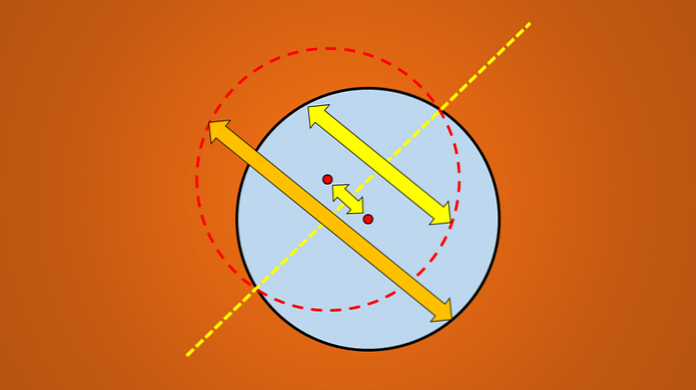
Ali ako se uzme u obzir sljedeća slika, dobro je poznato da je nacrtana linija os simetrije kruga.
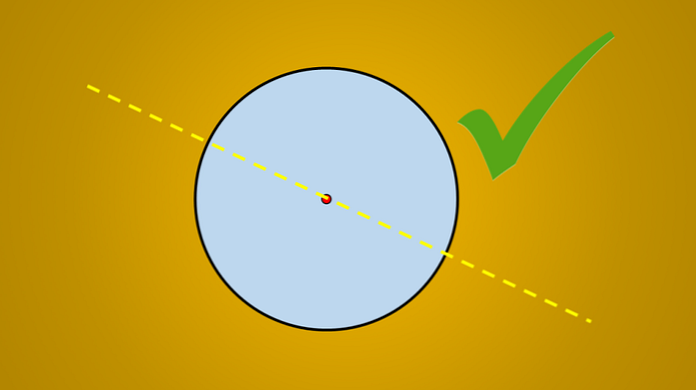
Pitanje je: ima li više osi simetrije? Odgovor je da. Ako okrenete ovu liniju 45 ° u smjeru suprotnom od kazaljke na satu, dobivena linija je također i os simetrije kruga.
Isto se događa ako zakrenete za 90 °, 30 °, 8 ° i općenito za bilo koji broj stupnjeva.
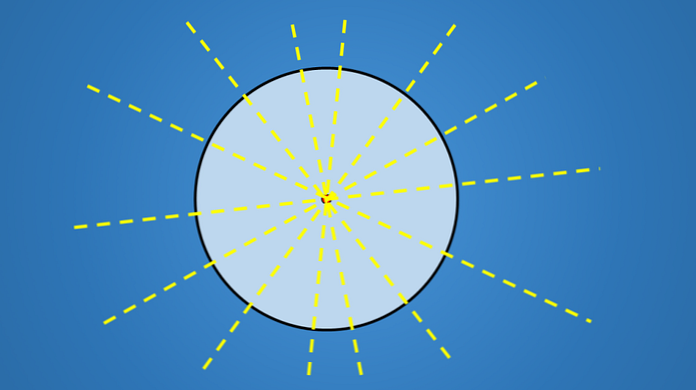
Važna stvar u tim redovima nije nagib koji imaju, već svi prolaze kroz središte kruga. Stoga je svaka linija koja sadrži promjer kruga os simetrije.
Dakle, budući da krug ima beskonačan broj promjera, onda ima beskonačan broj osi simetrije.
Druge geometrijske figure, kao što su trokut, četverokut, peterokut, šesterokut ili bilo koji drugi poligon, imaju konačan broj osi simetrije.
Razlog zašto krug ima beskonačan broj simetrijskih osi je taj što nema strane.
reference
- Basto, J.R. (2014). Matematika 3: Osnovna analitička geometrija. Patria Editorial Group.
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Matematika: pristup rješavanja problema za učitelje osnovnog obrazovanja. López Mateos Urednici.
- Bult, B., i Hobbs, D. (2001). Matematički leksikon (ilustrirano ed.). (F. P. Cadena, Trad.) Izdanja AKAL.
- Callejo, I., Aguilera, M., Martinez, L., i Aldea, C. (1986). Matematika. Geometrija. Reforma gornjeg ciklusa E.G.. Ministarstvo obrazovanja.
- Schneider, W., & Sappert, D. (1990). Praktični tehnički priručnik za crtanje: uvod u osnove industrijskog tehničkog crtanja. Reverte.
- Thomas, G. B., & Weir, M. D. (2006). Izračun: nekoliko varijabli. Obrazovanje Pearson.


