Formule kutnog pomaka i riješene vježbe

kutni pomak generira se kada se objekt kreće slijedeći put ili put koji ima oblik kruga. Ona se razlikuje od raseljavanja; dok kutni pomak mjeri prevaljeni kut, pomak mjeri udaljenost.

Za izračunavanje kutnog pomaka predmeta koji se kreće duž oboda mogu se koristiti dva načina: ako je početni i završni kut poznat, tada će kutni pomak biti oduzimanje između konačnog kuta i početnog kuta..

Ako je poznata duljina pomaka (duljina kružnog luka) i radijusa opsega, tada je kutni pomak dan θ = l / r..

indeks

• 1 Formule
• 2 vježbe
  • 2.1 Prva vježba
  • 2.2 Druga vježba
  • 2.3 Treća vježba
• 3 Reference

formula

Da biste dobili gore opisane formule, možete vidjeti sljedeće slike:

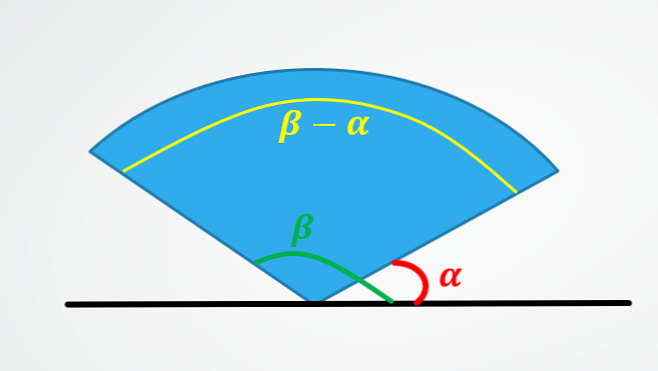
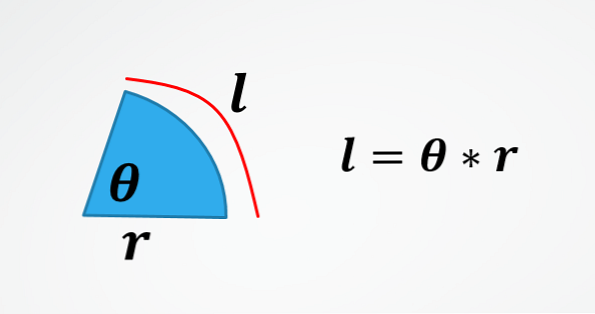
Prvi pokazuje zašto je kutni pomak jednak oduzimanju konačnog kuta minus početni kut.

U drugoj slici je formula za duljinu luka kružnice. Stoga, brisanjem θ dobivate formulu opisanu na početku.

trening

U nastavku su navedene neke vježbe u kojima treba primijeniti definiciju kutnog pomaka i gdje se koriste gore opisane formule.

Prva vježba

Juan je trčao na udaljenosti od 35 metara na kružnoj stazi čiji je polumjer jednak 7 metara. Izračunajte kutni pomak koji je napravio Juan.

otopina

Budući da je udaljenost prijeđenog luka i polumjer opsega poznata, druga formula može se primijeniti da bi se znalo o kutnom pomaku koji je napravio Juan. Koristeći gore opisanu formulu imate θ = 35/7 = 5 radijana.

Druga vježba

Ako imate da je Mario putovao u svojoj polovici kružne staze, kakav je kutni pomak učinio Mario??

otopina

U ovoj vježbi primijenit će se prva formula. Budući da je poznato da je Mario putovao pola staze, može se pretpostaviti da je startao u kutu od 0 °, a kada je stigao do sredine kruga, prešao je 180 °. Stoga je odgovor 180 ° -0 ° = 180 ° = π radijana.

Treća vježba

María ima kružni bazen. Vaš pas trči oko bazena na udaljenosti od 18 metara. Ako je polumjer bazena 3 metra, koliki je kutni pomak od Marijine maskote??

otopina

Budući da je bazen kružni i znate njegov polumjer, možete nastaviti s korištenjem druge formule.

Poznato je da je radijus jednak 3 metra, a udaljenost koju je prolazio ljubimac iznosi 18 metara. Stoga je izveden kutni pomak jednak θ = 18/3 = 6 radijana.

reference

1. Basto, J.R. (2014). Matematika 3: Osnovna analitička geometrija. Patria Editorial Group.
2. Billstein, R., Libeskind, S., & Lott, J.W. (2013). Matematika: pristup rješavanja problema za učitelje osnovnog obrazovanja. López Mateos Urednici.
3. Bult, B., i Hobbs, D. (2001). Matematički leksikon (ilustrirano ed.). (F. P. Cadena, Trad.) Izdanja AKAL.
4. Callejo, I., Aguilera, M., Martinez, L., i Aldea, C. (1986). Matematika. Geometrija. Reforma gornjeg ciklusa E.G.. Ministarstvo obrazovanja.
5. Schneider, W., & Sappert, D. (1990). Praktični tehnički priručnik za crtanje: uvod u osnove industrijskog tehničkog crtanja. Reverte.
6. Thomas, G. B., & Weir, M. D. (2006). Izračun: nekoliko varijabli. Obrazovanje Pearson.