Kolinearni sustav i primjeri

kolinearni vektori One su jedna od tri vrste postojećih vektora. Radi se o onim vektorima koji su u istom smjeru ili liniji djelovanja. To znači sljedeće: dva ili više vektora bit će kolinearni ako su raspoređeni u ravne linije koje su paralelne jedna s drugom.

Vektor se definira kao količina koja se primjenjuje na tijelo i karakterizira se kao da ima smjer, smisao i ljestvicu. Vektori se mogu naći u ravnini ili u prostoru i mogu biti različitih tipova: kolinearni vektori, konkurentni vektori i paralelni vektori.

indeks

• 1 kolinealni vektori
• 2 Značajke
  • 2.1 Primjer 1
  • 2.2 Primjer 2
  • 2.3 Primjer 1
• 3 Kolinearni vektorski sustav
  • 3.1. Kolinearni vektori s suprotnim osjetilima
  • 3.2. Kolinearni vektori s istim smislom
  • 3.3. Kolinearni vektori s jednakim veličinama i suprotnim osjetilima
• 4 Razlika između kolinearnih i istodobnih vektora
• 5 Reference

Kolinearni vektori

Vektori su kolinearni ako je linija djelovanja jednog jednaka liniji djelovanja svih drugih vektora, bez obzira na veličinu i smisao svakog od vektora..

Vektori se koriste kao prikazi u različitim područjima kao što su matematika, fizika, algebra i također u geometriji, gdje su vektori kolinearni samo kada je njihov smjer isti, bez obzira na to je li njihovo značenje.

značajke

- Dva ili više vektora su kolinearna ako je odnos između koordinata jednak.

Primjer 1

Imamo vektore m = m_x; m_y i n = n_x; n_y. To su kolinearne ako:

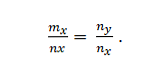
Primjer 2

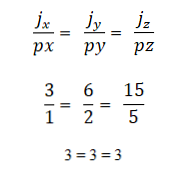
- Dva ili više vektora su kolinearna ako je umnožavanje proizvoda ili vektora jednako nuli (0). To je zbog toga što je u koordinatnom sustavu svaki vektor karakteriziran odgovarajućim koordinatama, a ako su one proporcionalne jedna drugoj, vektori će biti kolinearni. To se izražava kako slijedi:

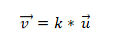
Primjer 1

Imamo vektore a = (10, 5) i b = (6, 3). Da bi se utvrdilo jesu li kolinearni, primjenjuje se teorija determinanta koja uspostavlja jednakost križnih proizvoda. Na taj način morate:

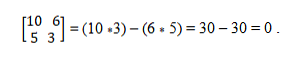
Kolinearni vektorski sustav

Kolinearni vektori prikazani su grafički koristeći smjer i smisao tih - uzimajući u obzir da moraju proći kroz točku primjene - i modul, koji je određena skala ili dužina.

Sustav kolinearnih vektora nastaje kada dva ili više vektora djeluju na objekt ili tijelo, koji predstavljaju silu i djeluju u istom smjeru.

Na primjer, ako se na tijelo primijene dvije kolinearne sile, rezultanta tih ovisnosti ovisit će samo o smjeru u kojem djeluju. Postoje tri slučaja:

Kolinearni vektori s suprotnim osjetilima

Rezultat dva kolinearna vektora jednak je zbroju tih:

R = = F = F₁ + F_2.

primjer

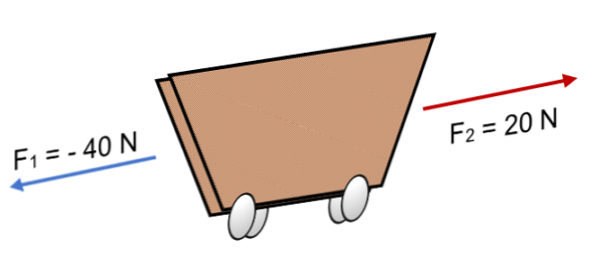
Ako dvije sile djeluju na košaricu F₁ = 40 N i F₂ = 20 N u suprotnom smjeru (kao što je prikazano na slici), rezultat je:

R = = F = (- 40 N) + 20N.

R = - 20 N.

Kolinearni vektori s istim smislom

Magnituda rezultirajuće sile bit će jednaka zbroju kolinearnih vektora:

R = = F = F₁ + F_2.

primjer

Ako dvije sile djeluju na košaricu F₁ = 35 N i F₂ = 55 N u istom smjeru (kao što je prikazano na slici), rezultat je:

R = = F = 35 N + 55N.

R = 90 N.

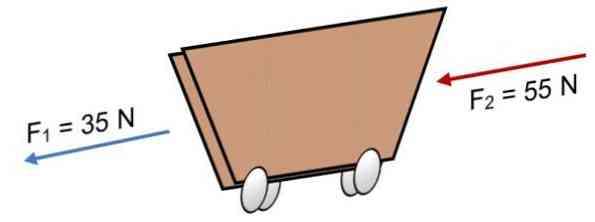
Pozitivan rezultat pokazuje da kolinearni vektori djeluju lijevo.

Kolinearni vektori jednakih veličina i suprotnih čula

Rezultat dva kolinearna vektora bit će jednak zbroju kolinearnih vektora:

R = = F = F₁ + F_2.

Budući da sile imaju istu veličinu, ali u suprotnom smjeru - to jest, jedna će biti pozitivna, a druga negativna - kada se dodaju dvije sile, rezultanta će biti jednaka nuli.

primjer

Ako dvije sile djeluju na košaricu F₁ = -7 N i F₂ = 7 N, koji imaju istu veličinu, ali u suprotnom smjeru (kao što je prikazano na slici), rezultat je:

R = = F = (-7 N) + 7N.

R = 0.

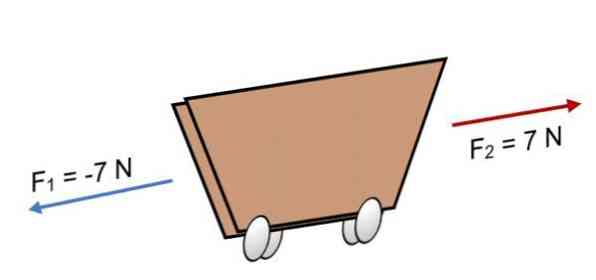
Budući da je rezultanta jednaka 0, to znači da su vektori međusobno uravnoteženi i stoga je tijelo u ravnoteži ili u mirovanju (neće se pomaknuti).

Razlika između kolinearnih i istodobnih vektora

Kolinearni vektori karakterizirani su time da imaju isti smjer na istoj liniji, ili zato što su paralelni s pravcem; to su vektori koji usmjeravaju paralelne linije.

S druge strane, paralelni vektori su definirani zato što su u različitim pravcima djelovanja koji se presreću u jednoj točki.

Drugim riječima, oni imaju istu točku podrijetla ili dolaska - bez obzira na njihov modul, smjer ili smjer -, formirajući kut između njih.

Sustavi istovremenih vektora rješavaju se matematičkim metodama ili grafovima, koji su metoda paralelograma sila i metoda poligona sila. Kroz njih će se odrediti vrijednost dobivenog vektora, što ukazuje na smjer u kojem će se tijelo kretati.

U osnovi, glavna razlika između kolinearnih vektora i istovremenih vektora je linija djelovanja u kojoj djeluju: kolinearne one djeluju u istoj liniji, dok istodobne u različitim.

To jest, kolinearni vektori djeluju u jednoj ravnini, "X" ili "Y"; i istodobno djeluju u obje ravnine, počevši od iste točke.

Kolinearni vektori nisu u točki, kao što to čine i istovremeni, jer su paralelni jedan s drugim.

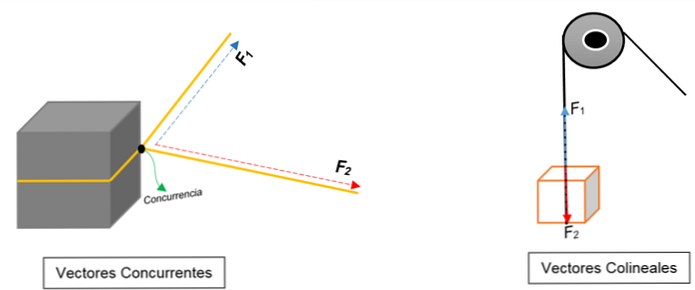
Na lijevoj slici možete vidjeti blok. Vezan je za uže, a čvor ga dijeli na dva dijela; kada se vuče prema različitim orijentacijama i različitim silama, blok će se pomaknuti prema istom smjeru.

Predstavljena su dva vektora koji se slažu u točki (bloku), bez obzira na njihov modul, smisao ili smjer.

Umjesto toga, na desnoj slici pojavljuje se koloturnik koji podiže kutiju. Uže predstavlja liniju djelovanja; kada se povuče, na nju djeluju dvije sile (vektori): jedna sila napetosti (pri penjanju na blok) i druga sila, ona koja vrši težinu bloka. Obje imaju isti smjer, ali u suprotnim smjerovima; ne slažete se u točki.

reference

1. Estalella, J.J. (1988). Vektorska analiza. Svezak 1.
2. Gupta, A. (s.f.). Tata McGraw-Hill obrazovanje.
3. Jin Ho Kwak, S.H. (2015). Linearna algebra. Springer znanost i poslovni mediji.
4. Montiel, H. P. (2000). Fizika 1 za tehnološku maturu. Patria Editorial Group.
5. Santiago Burbano de Ercilla, C.G. (2003). Opća fizika Uvodnik Tebar.
6. Sinha, K. (s.f.). Tekstovna matematika XII Vol 2. Rastogi Publikacije.