Koliko rubova ima heksagonalna prizma?

Znati koliko rubova ima šesterokutna prizma značenje "ruba", "prizme" i "heksagonala" mora biti poznato. Prva dva pojma su opće definicije, a treći pojam ima oblik geometrijske figure.

Kada govorimo o šesterokutu, spominje se šesterokut (poligon). Prefiks "hexa" označava da poligon ima šest strana.

Rub je rub predmeta. Geometrijski, to je linija koja povezuje dva uzastopna vertikala geometrijske figure.

Prizma je geometrijska figura ograničena s dvije baze koje su paralelne i jednake poligone, a njihove bočne strane su paralelogrami.

Na sljedećoj slici može se vidjeti da bočna lica šesterokutne prizme mogu biti pravokutnika, ali mogu biti i paralelogrami..

Prema vrsti paralelograma premije se mogu svrstati u dvije vrste: ravna i kosa.

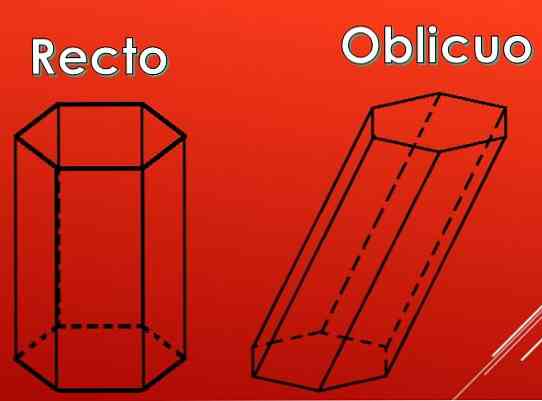
Kako brojati rubove šesterokutne prizme?

Broj rubova koje će imati heksagonalna prizma neće se promijeniti ako je u pitanju ravna ili kosa prizma. Također, broj rubova ne ovisi ni o duljini stranica.

Brojanje rubova šesterokutne prizme može se obaviti na nekoliko načina. Evo dva načina:

1. Razgradite prizmu

Jedan od načina za brojanje rubova je razgradnja šesterokutne prizme u njezine dvije baze i bočna lica. Na taj način dobivate dva šesterokuta i paralelogram s pet unutarnjih linija.

Svaki šesterokut ima šest rubova, tako da će prizma imati više od 12 rubova.

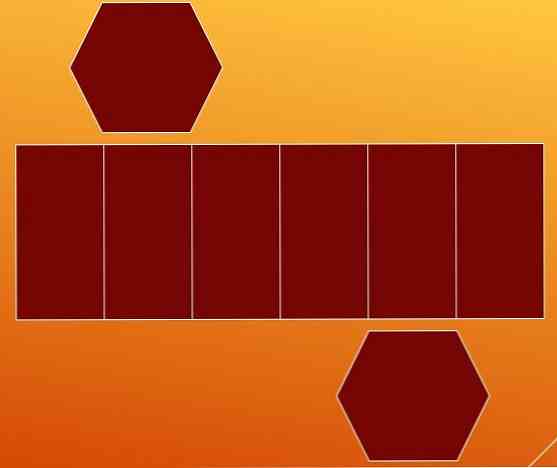
Na prvi pogled se smatra da paralelogram sadrži devet rubova (sedam okomitih i dva horizontalna). No, prikladno je prestati analizirati ovaj slučaj.

Kada se paralelogram savije u obliku prizme, može se vidjeti da će se prva linija s lijeve strane spojiti s posljednjom crtom na desnoj strani, kojom obje linije predstavljaju jedan rub..

Ali što je s dvije horizontalne linije?

Kada se svi dijelovi ponovno spoje, vodoravne linije će se spojiti, svaka sa šest rubova svakog šesterokuta. Zbog toga bi njihovo brojanje odvojeno bilo pogrešno.

Tako paralelogram sadrži šest rubova prizme koji zajedno s 12 rubova broje na početku, daje ukupno 18 rubova.

2.- Projiciranje svakog ruba

Drugi način, mnogo jednostavniji za brojanje rubova, koristi činjenicu da su baze šesterokutnih prizmi šesterokuti, a svaka baza ima šest rubova.

S druge strane, iz svakog vrha šesterokuta jedan se rub projicira na odgovarajući vrh drugog šesterokuta; to jest, postoji šest rubova koji se pridružuju jednoj bazi s drugom.

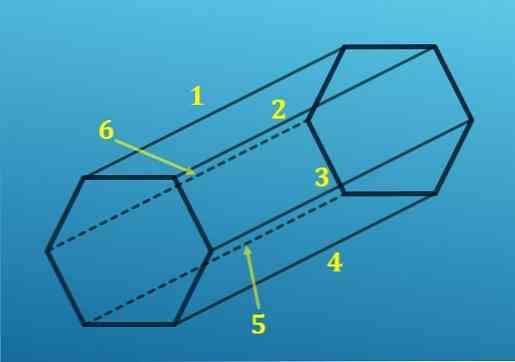
Dodavanjem svih rubova dobivate ukupno 18 rubova.

zaključak

Može se pokazati da je broj rubova prizme jednak trostrukom broju rubova koje ima poligon koji ima.

Stoga će peterokutna prizma imati 3 * 5 = 15 rubova, heptagonalna prizma će imati 3 * 7 = 21 rubova i tako će se moći primijeniti na bilo koju prizmu.

reference

1. Billstein, R., Libeskind, S., & Lott, J.W. (2013). Matematika: pristup rješavanja problema za učitelje osnovnog obrazovanja. López Mateos Urednici.
2. Fregoso, R.S., & Carrera, S.A. (2005). Matematika 3. Uređivanje Progreso.
3. Gallardo, G., i Pilar, P. M. (2005). Matematika 6. Uređivanje Progreso.
4. Gutiérrez, C.T. i Cisneros, M.P. (2005). 3. tečaj matematike. Uređivanje Progreso.
5. Kinsey, L., & Moore, T. E. (2006). Simetrija, oblik i prostor: Uvod u matematiku kroz geometriju (ilustrirano, reprint ed.). Springer znanost i poslovni mediji.
6. Mitchell, C. (1999). Dazzling Math Line dizajni (Ilustrirani ed.). Scholastic Inc.
7. R., M. P. (2005). Ja crtam 6º. Uređivanje Progreso.