Karakteristike kapilarnosti i primjer u vodi
kapilarnost To je svojstvo tekućina koje im omogućuju kretanje kroz cjevaste rupe ili porozne površine čak i protiv sile gravitacije. Za to mora postojati ravnoteža i koordinacija dvije sile povezane s molekulama tekućine: kohezija i adhezija; imaju ova dva fizička refleksija nazvana površinska napetost.
Tekućina mora biti u stanju navlažiti unutarnje stijenke cijevi ili pore materijala kroz koji se kreće. To se događa kada je sila adhezije (tekuća stijenka kapilarne cijevi) veća od intermolekularne kohezijske sile. Zbog toga molekule tekućine stvaraju jače interakcije s atomima materijala (staklo, papir, itd.) Nego između njih.
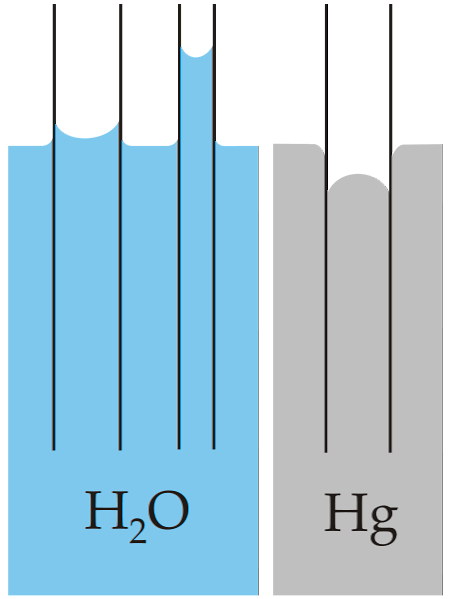
Klasični primjer kapilarnosti ilustriran je usporedbom ovog svojstva za dvije vrlo različite tekućine: vodu i živu.
Gornja slika pokazuje da se voda diže kroz zidove cijevi, što znači da ima veće sile prianjanja; dok se suprotno događa s živom, jer njezine kohezivne, metalne sile spajanja sprečavaju vlaženje stakla.
Zbog toga voda formira konkavni meniskus, a živa konveksni meniskus (u obliku kupole). Također treba napomenuti da što je manji polumjer cijevi ili dijela kroz koji se kreće tekućina, to je veća visina ili prijeđena udaljenost (usporedite visine vodenih stupova za obje cijevi).
indeks
- 1 Karakteristike kapilarnosti
- 1.1 - Površina tekućine
- 1.2 -Visina
- 1.3 - Površinska napetost
- 1.4 - Rad kapilare ili pora gdje se tekućina diže
- 1,5 - Kut kontakta (θ)
- 2 Kapilarnost vode
- 2.1 O biljkama
- 3 Reference
Obilježja kapilarnosti
-Površina tekućine
Površina tekućine, u vodi, u kapilari je konkavna; tj. meniskus je konkavan. Do te situacije dolazi zato što je rezultirajuće sile koje djeluju na molekule vode u blizini stijenke cijevi usmjerene na to.
U svim meniskusima postoji kontaktni kut (θ), koji je kut koji tvori stijenku kapilarne cijevi s linijom koja se dodiruje s površinom tekućine na mjestu kontakta.
Snage adhezije i kohezije
Ako sila adhezije tekućine na stijenku kapilara prevladava nad silom međumolekularne kohezije, tada je kut θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
Kada se kap vode stavi na površinu čistog stakla, voda se širi na staklo, tako da θ = 0 i cos θ = 1.
Ako sila intermolekularne kohezije prevladava nad jačinom prianjanja kapilare u tekućem zidu, na primjer u živu, menisk je konveksan, a kut θ ima vrijednost> 90 °; živa ne mokri kapilarni zid i stoga se spušta kroz svoj unutarnji zid.
Kad se kapljica žive stavi na površinu čistog stakla, kapljica zadržava svoj oblik i kut θ = 140º.
-visina
Voda se diže kroz kapilarnu cjevčicu do visine (h), u kojoj težina vodenog stupca kompenzira vertikalnu komponentu sile međumolekularne kohezije.
Kako se više vode diže, doći će točka u kojoj će gravitacija zaustaviti njezin rast, čak i kada površinska napetost djeluje u vašu korist.
Kada se to dogodi, molekule ne mogu nastaviti "penjati" se unutarnjim zidovima, a sve fizičke sile su izjednačene. S jedne strane imate sile koje potiču uzdizanje vode, as druge strane vlastita težina gura je dolje.
Jurinov zakon
To se može napisati matematički na sljedeći način:
2 π rΥcosθ = ρgπr2h
Gdje lijeva strana jednadžbe ovisi o površinskoj napetosti, čija je veličina također povezana s kohezijskim ili intermolekularnim silama; Cosθ predstavlja kontaktni kut, a radijus rupe kroz koju se diže tekućina.
A na desnoj strani jednadžbe imamo visinu h, silu gravitacije g i gustoću tekućine; to bi bila voda.
Brisanje onda h imate
h = (2Υcosθ / ρgr)
Ova formulacija je poznata kao Jurinov zakon, koji definira visinu koja doseže stupac tekućine, u kapilarnoj cijevi, kada je težina stupca tekućine uravnotežena s silom uskrsnuća kapilarno.
-Površinska napetost
Voda je dipolarna molekula, zbog elektronegativnosti atoma kisika i njegove molekularne geometrije. To uzrokuje da je dio molekule vode gdje se nalazi kisik negativno nabijen, dok je dio molekule vode, koji sadrži 2 atoma vodika, pozitivno nabijen..
Molekule unutar tekućine međusobno djeluju zahvaljujući višestrukim vodikovim vezama, držeći ih zajedno. Međutim, molekule vode koje se nalaze u međupovršini vode: zrak (površina), podložne su neto privlačenju molekula tekućeg sinusa, koje nije kompenzirano slabom privlačnošću molekulama zraka..
Prema tome, molekule vode sučelja podvrgnute su privlačnoj sili koja teži uklanjanju molekula vode iz sučelja; to jest, vodikovi mostovi formirani s molekulama u dnu povlače one koji su na površini. Prema tome, površinska napetost nastoji smanjiti površinu sučelja vode: zrak.
Odnos s h
Ako pogledate jednadžbu Jurinova zakona, naći ćete da je h izravno proporcionalan; dakle, što je veća površinska napetost tekućine, veća je visina koja može rasti kroz kapilaru ili poru materijala.
Stoga se može očekivati da se za dvije tekućine A i B, s različitim površinskim napetostima, ona s najvećom površinskom napetošću uzdiže na višu visinu..
Iz ove se točke može zaključiti da je visoka površinska napetost najvažnija karakteristika koja definira kapilarno svojstvo tekućine.
-Radijus kapilare ili pora gdje se tekućina diže
Promatranje Zakona Jurina ukazuje da je visina koju je dostigla tekućina u kapilari ili porama obrnuto proporcionalna radijusu iste.
Stoga, što je manji radijus, to je veća visina koju će stupac tekućine doseći kapilarnim djelovanjem. To se može vidjeti izravno na slici gdje se voda uspoređuje sa živom.
U staklenoj cijevi u radijusu polumjera 0.05 mm vodeni stupac kapilarnošću će doseći visinu od 30 cm. U kapilarnim cijevima radijusa od 1 μm s usisnim tlakom 1,5 x 103 hPa (što je jednako 1,5 atm) odgovara izračunu visine vodenog stupca od 14 do 15 m.
To je vrlo slično onome što se događa s onim slamkama koje se nekoliko puta okreću. Usisavanjem tekućine nastaje razlika u tlaku zbog koje se tekućina izdiže u usta.
Maksimalna vrijednost visine stupca postignuta kapilarnošću je teoretska, budući da se radijus kapilara ne može smanjiti iznad određene granice.
Zakon Poiseuillea
Time se utvrđuje da je protok stvarne tekućine dan sljedećim izrazom:
Q = (πr4/ 8ηl) ΔP
Gdje je Q protok tekućine, η je njegova viskoznost, l dužina cijevi, a ΔP razlika tlaka.
Kada se smanjuje radijus kapilare, visina stupca tekućine dostignuta kapilarnošću treba da se povećava neograničeno. Međutim, Poiseuille ističe da smanjenje radijusa također smanjuje protok tekućine kroz tu kapilaru.
Osim toga, viskoznost, koja je mjera otpornosti koja se suprotstavlja protoku stvarne tekućine, dodatno bi smanjila protok tekućine.
-Kut kontakta (θ)
Što je viša vrijednost cosθ, veća je visina stupca vode kapilarnošću, kao što je naznačeno Jurinovim zakonom.
Ako je θ mali i približava se nuli (0), cosθ je = 1, tako da će vrijednost h biti maksimalna. Naprotiv, ako je θ jednako 90º, cosθ = 0 i vrijednost h = 0.
Kada je vrijednost θ veća od 90º, što je slučaj s konveksnim meniskom, tekućina se ne povećava kapilarno i njezina je tendencija spuštanje (kao što se događa s živom).
Kapilarnost vode
Voda ima površinsku napetost od 72,75 N / m, relativno veliku u odnosu na vrijednosti za površinsku napetost sljedećih tekućina:
-Aceton: 22,75 N / m
-Etilni alkohol: 22,75 N / m
-Heksan: 18,43 N / m
-Metanol: 22,61 N / m.
Stoga voda ima iznimnu površinsku napetost, što pogoduje razvoju kapilarnog fenomena koji je nužan za apsorpciju vode i hranjivih tvari iz biljaka..
Na biljke

Kapilarnost je važan mehanizam za podizanje soka u ksilemu biljaka, ali sam po sebi nije dovoljan da sok dosegne lišće stabala..
Transpiracija ili isparavanje je važan mehanizam u usponu soka na ksilemu biljaka. Lišće gubi vodu isparavanjem, stvarajući smanjenje količine molekula vode, što uzrokuje privlačnost molekula vode prisutnih u kapilarnim cjevčicama (ksilem).
Molekule vode ne djeluju nezavisno jedna od druge, već djeluju na Van der Waalsove sile, što uzrokuje njihovo uzdizanje povezano s kapilarnim cjevčicama biljaka prema lišću.
Osim ovih mehanizama, treba napomenuti da biljke apsorbiraju vodu iz tla osmozom i da pozitivni tlak stvoren u korijenu pokreće početak uspona vode kroz kapilare biljke..
reference
- García Franco A. (2010). Površne pojave. Preuzeto s: sc.ehu.es
- Površinske pojave: površinska napetost i kapilarnost. [PDF]. Dobavljeno iz: ugr.es
- Wikipedia. (2018.). Kapilarnost. Preuzeto s: en.wikipedia.org
- Risvhan T. (s.f.) Kapilarnost u biljkama. Preuzeto s: academia.edu
- Helmenstine, Anne Marie, Ph.D. (22. prosinca 2018.) Kapilarna akcija: definicija i primjeri. Preuzeto s: thoughtco.com
- Ellen Ellis M. (2018). Kapilarno djelovanje vode: Definicija i primjeri. Studija. Preuzeto s: study.com
- Zaposlenici ScienceStruck. (16. srpnja 2017.) Primjeri koji objašnjavaju pojam i značenje kapilarnog djelovanja. Preuzeto s: sciencestruck.com


