Značajke heptagonalne prizme i kako izračunati volumen
heptagonalna prizma je geometrijska figura koja, kao što ime implicira, uključuje dvije geometrijske definicije koje su: prizma i heptagon.
"Prizma" je geometrijska figura ograničena dvjema bazama koje su jednaki i paralelni poligoni, a njihove bočne strane su paralelogrami.
"Heptagon" je poligon koji je formiran sa sedam (7) strana. Budući da je heptagon poligon, moguće je da je on pravilan ili nepravilan.
Za poligon se kaže da je pravilan ako su sve njegove strane jednake duljine i njihovi unutarnji kutovi mjere isto, također se nazivaju jednakostraničnim poligonima; inače se kaže da je poligon nepravilan.

Značajke heptagonalne prizme
Slijedi određena obilježja koja imaju heptagonalnu prizmu kao što su: njezina konstrukcija, svojstva baza, površina svih njezinih lica i njen volumen.
1. Izgradnja
Za izgradnju sedmerokutne prizme potrebna su dva heptagona, koja će biti njezine baze i sedam paralelograma, po jedan na svakoj strani šesterokuta.
Počnite crtanjem heptagon, zatim nacrtajte sedam vertikalnih linija, jednake duljine, koje dolaze iz svakog od njegovih vrhova.
Konačno je nacrtan još jedan heptagon tako da se njegovi vrhovi poklapaju s krajem crta nacrtanih u prethodnom koraku.
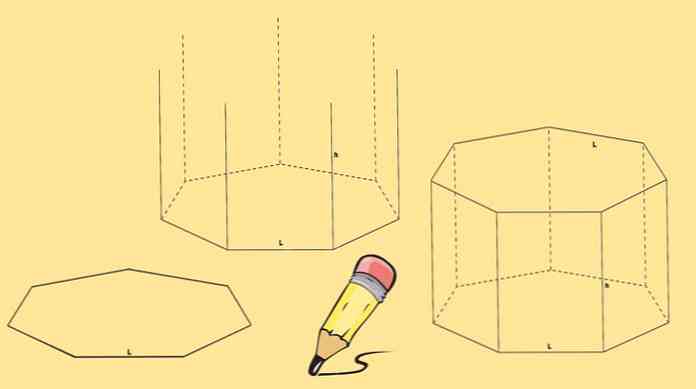
Gore prikazana heptagonalna prizma naziva se ravna heptagonalna prizma. Ali također možete imati kosu heptagonalnu prizmu poput one na sljedećoj slici.

2. Svojstva baza
Budući da su njihove baze heptagoni, oni odgovaraju da je dijagonalni broj D = nx (n-3) / 2, gdje je "n" broj strana poligona; u ovom slučaju imamo D = 7 × 4/2 = 14.
Također možemo vidjeti da je zbroj unutarnjih kutova bilo kojeg heptogona (regularnog ili nepravilnog) jednak 900º. To se može potvrditi sljedećom slikom.
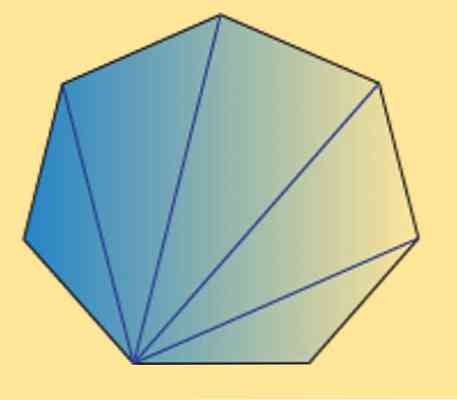
Kao što možete vidjeti, postoji 5 unutarnjih trokuta, a koristeći zbroj unutarnjih kutova trokuta jednak je 180º, može se dobiti da željeni rezultat.
3. Prostor potreban za izgradnju heptagonalne prizme
Budući da su njegove baze dvije heptagone i njegove strane su sedam paralelograma, površina potrebna za konstrukciju heptagonalne prizme jednaka je 2xH + 7xP, gdje je "H" površina svakog heptagona i "P" područje svakog paralelograma.
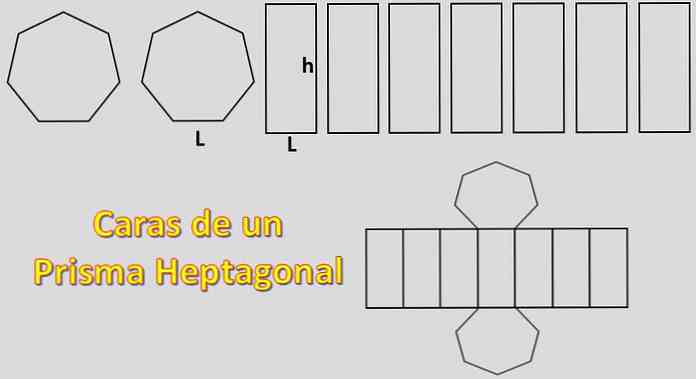
U tom slučaju, izračunat će se područje regularnog heksagona. Za to je važno znati definiciju apoteme.
Apothem je okomita linija koja ide od središta regularnog poligona do sredine bilo koje njegove strane.
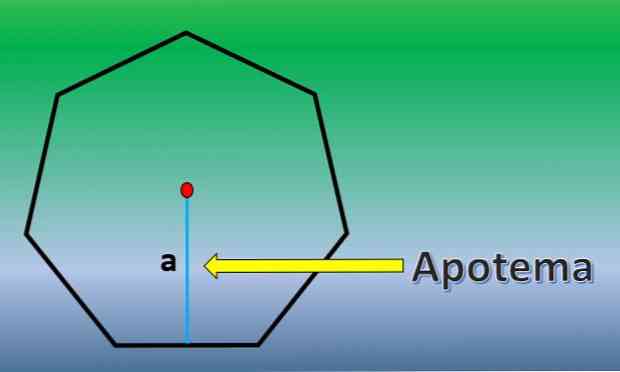
Jednom kada je apotem poznat, područje heptagona je H = 7xLxa / 2, gdje je "L" dužina svake strane i "a" dužina apotema..
Područje paralelograma je lako izračunati, a definira se kao P = Lxh, pri čemu je "L" jednaka duljina bočne strane šesterokuta i "h" je visina prizme.
U zaključku, količina materijala potrebnog za izgradnju heptagonalne prizme (s pravilnim bazama) je 7xLxa + 7xLxh, to jest, 7xL (a + h).
4. Glasnoća
Jednom kada je područje baze i visina prizme poznato, volumen je definiran kao (osnovna površina) x (visina).
U slučaju heptagonalne prizme (s regularnom bazom) ona ima svoj volumen V = 7xLxaxh / 2; Također se može napisati kao V = Pxaxh / 2, gdje je "P" perimetar regularnog heptagona.
reference
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Matematika: pristup rješavanja problema za učitelje osnovnog obrazovanja. López Mateos Urednici.
- Fregoso, R.S., & Carrera, S.A. (2005). Matematika 3. Uređivanje Progreso.
- Gallardo, G., i Pilar, P. M. (2005). Matematika 6. Uređivanje Progreso.
- Gutiérrez, C.T. i Cisneros, M.P. (2005). 3. tečaj matematike. Uređivanje Progreso.
- Kinsey, L., & Moore, T. E. (2006). Simetrija, oblik i prostor: Uvod u matematiku kroz geometriju (ilustrirano, reprint ed.). Springer znanost i poslovni mediji.
- Mitchell, C. (1999). Dazzling Math Line dizajni (Ilustrirani ed.). Scholastic Inc.
- R., M. P. (2005). Ja crtam 6º. Uređivanje Progreso.


